试卷结构
(一)题分及考试时间
试卷满分为150分,考试时间为180分钟.
(二)内容比例
高等教学 约78%
线性代数 约22%
(三)题型比例
填空题与选择题 约37%
解答题(包括证明题) 约63%
新大纲变化:填空选择题由37%改为45%,解答题由55%改为63%。
解析与预测:由题型比例的变化可以看出,填空选择题目的数量变化到了06年时的情形,客观题目(选择题、填空题)的比例降低,预计填空题会由原来的10个到08年考试时的8个,主观题目增加了比重,预计在解答当中增加一个高等的题目。
变化的目的:考研题型主观题目的增加说明了考研数学题目要增加对同学们的知识的综合分析与计算能力的考查,增加大家选择知识点的判断能力及对题型的熟练运用等方面的能力。更加体现了研究生考试是选拔性考试的特点。
应对策略:大家在复习的时候要注意积累对综合题目的总结与提炼,将典型的数学题目的题型或者解题思想上升到一半的理论,总结成自己容易记忆的适合自己的解题方法。比如:用泰勒公式求极限的题目,看到含有5个基本泰勒公式求极限时,要想到用泰勒公式的含有皮亚诺型余项公式来求。
高等数学
第一章、函数、极限、连续
考试内容:函数的概念及表示法 函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形 初等函数 函数关系的建立 数列极限与函数极限的定义及其性质 函数的左极限和右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限:
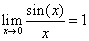 ,
, 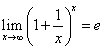
函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质
考试要求:
1. 理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系
2. 了解函数的有界性、单调性、周期性和奇偶性
3. 理解复合函数及分段函数的概念了解反函数及隐函数的概念
4. 掌握基本初等函数的性质及其图形,了解初等函数的概念
5. 理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左、右极限之间的关系
6. 掌握极限的性质及四则运算法则
7. 掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.
8. 理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限,
9. 理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型
10. 了解连续函数的性质和初等函数一的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.
第二章:一元函数微分学
考试内容:导数和微分的概念 导数的几何意义和物理意义 函数的可导性与连续性之间的关系 平面曲线的切线和法线 导数和微分的四则运算 基本初等函数的导数 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法 高阶导数 一阶微分形式的不变性 微分中值定理 洛必达(L'Hospital)法则 函数单调性的判别 函数的极值 函数图形的凹凸性、拐点及渐近线 函数图形的描绘 函数的最大值和最小值 弧微分 曲率的概念 曲率圆与曲率半径
考试要求:
1. 理解导数和微分的概念,理解导数和微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.
2. 掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分
3. 了解高阶导数的概念,会求简单函数的高阶导数
4. 会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数
5. 理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理
6. 掌握用洛必达法刚求未定式极限的方法.
7. 理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.
8. 会用导数判断函数图形的凹凸性(注:在区间(a,b)内,设函数f(x)具有二阶导数。当f``(x)>0时,f(x)的图形是凹的;当f``(x)<0时,f(x)的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.
9. 了解曲率、曲率圆和曲率半径的概念,会计算曲率和曲率半径.
新大纲变化:一元函数微分学部分新加了两个知识点(1) 曲率圆(2) 函数图形凸凹性的判断
解析及应对策略:在原来对曲率以及曲率半径的概念以及计算掌握上,新添加了曲率圆,实际上有曲率半径就肯定对应有一个相应的曲率圆,所以曲率圆可以当作是曲率半径的延伸,这个知识点地增加从考试要求上难度并没有增加。大家可以注意到,虽然在考试内容中提到了曲率圆的概念,但在考试要求中却并未强调对该知识点的应用,只是对概念要求了解。大纲做这样的调整,只是为了完善我们的知识体系。大家在复习曲率有关内容的时候,心中一定要有曲率圆这样一个概念,把曲率圆也要加入到相关的题目当中,从整体上去把握。
新大纲在原有凸凹性要求的基础上进一步强调了凸凹性的判断方法,首先明确大纲做这样的修订与往年相比没有也不会增加难度,但是由于突出强调这个判断方法,除了使叙述更加规范外,更强调了用函数导数判断凹凸性的重要性,有可能会在此问题上用选择填空形式来考核同学们对该知识点的理解。函数的凸凹性本来就是非常重要的一项内容也是经常考到的内容,所以,需要我们在复习这部分内容的时候特要多理解,多练习,多总结。
第三章:一元函数积分学
考试内容
原函数和不定积分的概念 不定积分的基本性质 基本积分公式 定积分的概念和基本性质 定积分中值定理 积分上限的函数及其导数 牛顿-莱布尼茨(Newton-Leibniz)公式 不定积分和定积分的换元积分法与分部积分法 有理函数、三角函数的有理式和简单无理函数的积分 反常(广义)积分 定积分的应用
考试要求
1. 理解原函数的概念,理解不定积分和定积分的概念
2. 掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法
3. 会求有理函数、三角函数有理式和简单无理函数的积分
4. 理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式
5. 了解反常积分的概念,会计算反常积分
6. 掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值
新大纲变化:一元函数积分学部分新加了一个知识点:用定积分表达和计算几何量“形心”
解析与应对策略: 08年大纲在原有要求掌握用定积分表达和计算一些几何量与物理量的基础上,加入了用定积分计算几何量“形心”。客观地说这个新知识点,是一元函数积分学在实际中应用中的拓广。在复习相关内容上要注意相似概念的区别。比如:形心的定义及与重心的区别。形心:物体的几何中心(只与物体的几何形状和尺寸有关,与组成该物体的物质无关)。重心:物体的重力的合力作用点称为物体的重心(与组成该物体的物质有关)。大家在掌握形心定义的基础上要记忆各种坐标系以及各种情况下的计算公式,平时练习的过程中多运算,提高自己在这方面的熟练程度。
第四章:多元函数微积分学
考试内容
多元函数的概念 二元函数的几何意义 二元函数的极限与连续的概念 有界闭区域上二元连续函数的性质 多元函数的偏导数和全微分 多元复合函数、隐函数的求导法 二阶偏导数 多元函数的极值和条件极值、最大值和最小值 二重积分的概念、基本性质和计算
考试要求
1. 了解多元函数的概念,了解二元函数的几何意义
2. 了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质
3. 了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数
4. 了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并求解一些简单的应用题.
5. 了解二重积分的概念与基本性质,掌握二重积分(直角坐标、极坐标)的计算方法
第五章:常微分方程
考试内容
常微分方程的基本概念 变量可分离的微分方程 齐次微分方程 一阶线性微分方程 可降阶的高阶微分方程 线性微分方程解的性质及解的结构定理 二阶常系数齐次线性微分方程 高于二阶的某些常系数齐次线性微分方程 简单的二阶常系数非齐次线性微分方程 微分方程的简单应用
考试要求
1. 了解微分方程及其阶、解、通解、初始条件和特解等概念
2. 掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程
3. 会用降阶法解下列形式的微分方程: 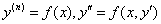 和
和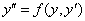
4. 理解二阶线性微分方程解的性质及解的结构定理.
5. 掌握二阶常系数齐次
【下一页】













